FSSのIRT
まず、9 人の FSS 被験者を使用して GRM IRT を実行しました。 スクリープロットで確認した結果、遷移固有値は5.85~1.18と0.44~0.39の間であり、1次元と考えられました。 項目パラメータの数を推定した後、項目ごとに ICC、IIC、TIF を確認しました。
ICC の結果では、すべての項目において 7 年生の回答確率が 6 年生の回答確率のピーク前に増加しており、6 年生と 7 年生の差は高いレベルの疲労を反映していないことが示されました。 特に、項目 1 と 2 では、疲労強度に対するスコアの交互作用確率がピークにならず、ばらつきが大きいことが確認されました。 項目 1 と 2 には疲労度に関する情報がほとんど含まれていません。 また、項目 3 は疲労が比較的弱い場合でも情報量が多く、その他の項目は疲労が中程度から強い場合に反応が高いことがわかりました。 IIC の結果は、項目 1 と 2 の情報量が疲労度に関して一律に低いことを示しました。 項目 3 には、項目 1 と 2 を除く他の項目よりも情報が少なくなっています。
これらの調査結果に基づいて、次の 3 つの追加条件が検討されました。(1) 第 1 項および第 2 項の削除。 (2) 行 6 と行 7 をマージします。 (3) (1)と(2)を両方行います。 いずれの場合も一次元性が確認された。 条件 1 では、グレード 6 とグレード 7 が区別できず、ICC の結果と同様の問題が残りました。 条件 2 では、IIC は項目 1 と 2 の情報量が疲労強度に関して均一に分布していることを示しました (図 S2 と S3)。 さらに、条件 1 のみが他の条件よりも低い TIF を示しました。
条件 3 の ICC、IIC、TIF を図 1 に示します。ICC から、スコア反応確率と疲労重症度との間に一致が見られ、IIC は疲労重症度の特定の領域で情報量が増加していることを示しました。 TIFについては、オリジナルFSSの7項目中6段階の条件設定では低下は見られず、情報損失量も限定的であった。 したがって、以下に報告される結果は、条件 3 で FSS を使用して達成されました (たとえば、項目 1 と 2 が削除され、行 6 と 7 が結合されました)。
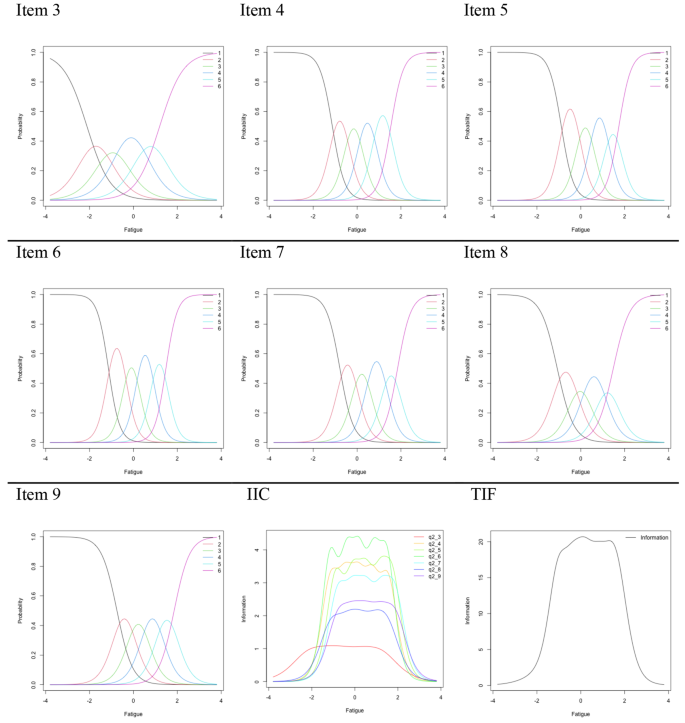
条件 3 の項目特性曲線、項目情報曲線、およびテスト情報関数。ケース 3 では、項目 1 と 2 が削除され、行 6 と 7 がマージされました。ICC: 項目特性曲線、IIC: 項目情報曲線、TIF: テスト情報関数
IRTが判定した各項目を平均して算出したスコアと、IRTが判定した各項目の難易度係数を用いて算出したスコアとの相関係数は非常に高かった(s= .99、 s <.001 [from fss x fss_irt])。 項目の平均値をスコアの計算に使用した場合、スコアはほぼ同一であったため、FSS スコア (FSS) [IRT])調査の尺度の都合上、IRT が定めた 7 項目 6 段階評価の平均値から算出。 元の FSS と FSS (IRT) の相関は高かった (s= .97、 s<.001)。
記述統計
表 1 は 692 名の参加者の特徴を示しています。 スケールの記述統計を表 2 に示します。すべてのスケールの学年内相関が高かった。 ただし、FSS (IRT) は 0.59 と比較的低かったです。
ストレスと疲労の関係
一元配置分散分析を実行して、精神的および肉体的なストレス状態と疲労の関係を調べました。 独立変数は、精神的および身体的ストレス状態の存在でした。 結果を表 2 に示します。ANOVA 結果で有意であることが判明した変数に対して多重比較 (Tukey の正直有意差検定) も実行し、95% CI を表 3 に示します。
MFI の場合、重要な ANOVA の結果 (F [3, 619]= 21.14、 s<.001、 コーエン= 0.32)。 複数の比較により、グループ 4 (ストレスのない環境) では、(s– グループ 1 (精神的にストレスの多い環境) とグループ 3 (精神的および肉体的にストレスの多い環境) の値 <0.001)。
一元配置分散分析の結果は、FSS (IRT) にとって有意でした (F (3, 619) = 19.84、 s<.001、 コーエン= 0.31)。 多重比較により、グループ 4 はグループ 1 およびグループ 3 よりも低かったことが示されました (s– 値 < 0.001); したがって、同じグループでも、MFI と FSS (IRT) の両方の結果に有意な差があることが判明しました。
睡眠時間と疲労の関係
一元配置分散分析を実行して、週の平均睡眠時間と疲労の関係を調べました。 独立変数は、1 週間あたりの平均睡眠時間を「4 時間未満」から「9 時間以上」まで 1 時間単位で表す 7 レベルのカテゴリ変数でした。 図 2 は、MFI および FSS スコア (IRT) と睡眠時間の関係を示しています。 MFI の場合、グループ 1 (<4 時間) とグループ 7 (9 時間以上) では、より高いスコアで進行性の U 字型移行が明らかになりました。
MFI については、ANOVA の結果が重要であることがわかりました (F [6, 616]= 5.862、 s<.001、 コーエン= 0.17)。 複数の比較により、グループ 1 (<4 時間) とグループ 2 (4 ~ 5 時間) の方が有意に高いことが明らかになりました。s-値 < 0.01、95% 信頼区間 [CIs] = [-22.02 -1.48]) グループ 3、4、および 5 (6 ~ 8 時間)。 FSS の結果は、MFI 曲線と同様の U 字型曲線を示しました。 ANOVA の結果は有意でした (F [6, 616]= 2.87、 s<.01、 コーエン= 0.17)。 複数の比較により、グループ 1 がグループ 3 および 4 よりも優れていることが実証されました (s– 値 <0.05)。

睡眠時間コホート別の多次元疲労インベントリと疲労重症度スケールの箱ひげ図。 MFI: 多次元疲労インベントリ、FSS: 疲労重症度スケール。 睡眠神話: 1、4 時間未満。 2、4~5時間。 3、5~6時間。 7、9時間以上。 ハイフンの右側に示されている睡眠時間はグループには含まれませんが、次のグループに含まれます(つまり、グループ 2 には睡眠時間が 4 時間以上 5 時間未満の人が含まれます)。 * s<.05、** s<.01、*** s<.001
相関分析
FSS (IRT) と MFI は中程度の相関関係を示しました (s= .62、 s< .001) 相互および PHQ-9 (MFI: s= .62、 s< .001; FSS [IRT]: s= .52、 s<.001)。
回帰分析
重回帰分析は、PHQ-9 を従属変数として、疲労の測定値を独立変数として使用して実行されました。 平均 s2 この形式の値は 0.410 でした。 標準化された偏回帰係数は、MFI の方が大幅に高かった (β= 0.479、 R= 12.83、95% CI =[0.406 0.553]と s< .001) および FSS (IRT) (β= 0.222、 R= 5.94、95% CI =[0.149 0.295]と s< 001)、MFI の値は FSS (IRT) の値よりも高かった。 コントラスト膨張係数 (VIF) は 1.63 でした。
相互効果モデルを使用した疲労とうつ病の関連性
交差効果モデルを実行して、2つの時点で一致する125人の個人からのデータを使用して、疲労とうつ病の間の時系列および前後の関係をテストしました(図S5)。 MFI と PHQ-9 (図 S5a) では、FSS (IRT) と PHQ-9 (図 S5b) の両方が飽和モデルでした。 MFI については、タイム 2 PHQ-9 でタイム 1 MFI から顕著なプラスの効果がありました (β= 0.251、 s<.001); 誤差の共分散も大幅に高くなりました。 FSS (IRT) の有意なプラスの効果が、時間 2 から PHQ-9 で確認されました (β= 0.116、 s< .05); 誤差の分散もはるかに大きくなりました。
同時効果モデルを用いた疲労とうつ病の関連性
相互効果モデルでは、誤差の共分散が大幅に高くなりました。 したがって、時刻 2 の変数は、時刻 (1) で決定された変数以外の変数によって大きく影響されている可能性が考えられます。要因の 1 つは、時刻 1 と時刻 2 の間の測定間隔が約 18 日であることです。 これは、大きな時間分散 (2) を説明するには期間が離れすぎている可能性があることを意味するため、同時効果モデルも調べました (図 3)。

同時効果モデルの結果。 注意。 N = 125。MFI: 多次元疲労インベントリ、FSS: 疲労重症度スケール、PHQ-9: 患者健康質問票、t1: 時間 1、t2: 時間 2。 *** s<.001
MFI と PHQ-9 (図 3a) の場合、品質指標は許容範囲内でした (χ2(1) = 1.907、 nsと グフィ= 0.992、 AGFI= 0.922、 CFI= 0.998、 RMSEA= 0.085)、タイム 2 PHQ-9 におけるタイム 2 MFI の有意なプラスの効果が確認されています (β= 0.258、 s<.001)。 さらに、タイム 2 PHQ-9 のタイム 2 MFI への影響は有意ではないことが判明しました (β= 0.060、 ns)。
同様の FSS アッセイ (IRT) も実行されました (図 3b)。 適合指標の品質が許容できませんでした (χ2(1) = 5.259、 s<.05、 グフィ= 0.979、 AGFI= 0.793、 CFI= 0.985、 RMSEA= 0.185)、モデルがデータに適合しない可能性があることを示しています。 時間 2 の PHQ-9 に対する時間 2 FSS (IRT) の影響は有意ではありませんでした (β= -0.008、 ns)。 ただし、時間 2 の PHQ-9 の時間 2 FSS (IRT) に対する有意なプラスの効果が確認されました (β= 0.472、 s<.001)。

「音楽マニア。プロの問題解決者。読者。受賞歴のあるテレビ忍者。」


More Stories
JGB Curveは、日本の金融の健康に関する懸念の中で認めています – TradingViewニュース
週末の睡眠を補うことで心臓病のリスクが5分の1減少する可能性がある――研究 |心臓病
化石によると、先史時代のカイギュウはワニとサメに食べられた